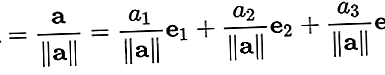Wektor w matematyce i fizyce można zdefiniować jako obiekty geometryczne, które mają wielkość i kierunek. Wektor jest przedstawiony za pomocą strzałki, gdzie podstawa strzałki wskazuje punkt zaczepienia (punkt początkowy) wektora, długość strzałki wskazuje rozmiar lub wartość wektora (im dłuższa strzałka, tym większa wartość lub wartość wektora i odwrotnie), natomiast strzałka wskazuje kierunek wektora.

Na piśmie, jeśli wektor zaczyna się w punkcie A i kończy w punkcie B, to można go zapisać małą literą, nad którą znajduje się linia / strzałka, jak 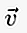 lub
lub 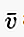 lub też:
lub też:
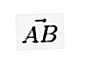
Rodzaje wektorów
Wektor w matematyce dzieli się na 4 typy, w tym:
Wektor pozycji
Wektor, którego punkt początkowy znajduje się w punkcie 0 (0,0), a jego koniec to A (a1, a2).
Wektor zerowy
„Wektor zero” (wektor zerowy lubwektor zerowy) jest wektorem, którego długość wynosi „zero”. Zapis w tej współrzędnej wektora to (0,0,0) i zwykle jest oznaczony symbolem  lub0. Ten wektor różni się od innych wektorów tym, że nie można go znormalizować (tzn. Żaden wektor jednostkowy nie jest wielokrotnością wektora zerowego). Liczba wektorów wynosi zero dla dowolnego wektoraza jestza (to jest,0+za=za).
lub0. Ten wektor różni się od innych wektorów tym, że nie można go znormalizować (tzn. Żaden wektor jednostkowy nie jest wielokrotnością wektora zerowego). Liczba wektorów wynosi zero dla dowolnego wektoraza jestza (to jest,0+za=za).
Wektor zerowy nie ma wyraźnego kierunku wektora.
Wektor jednostkowy
jest wektorem o długości „jeden”. Zwykle wektor jednostkowy służy tylko do wskazania kierunku. Wektor dowolnej długości można podzielić przez długość, aby uzyskać wektor jednostkowy. Nazywa się to „normalizacją” wektora. Wektor jednostkowy jest często oznaczany „czapką” nad małą literą „a”, jak wza.
Aby znormalizować wektorza = [za1, za2, za3], podziel wektor przez długość ||za||. Więc:
Wektor bazowy
Wektor jednostkowy, który jest prostopadły do siebie. W dwuwymiarowym wektorze przestrzennym (R2) ma mianowicie dwa wektory bazowe 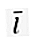 = (1, 0) i
= (1, 0) i 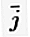 = (0, 1).
= (0, 1).
Podobieństwo dwóch wektorów
Mówi się, że dwa wektory są takie same, jeśli mają tę samą długość i kierunek

Wyrównanie dwóch wektorów
Dwa wektory nazywane są równoległymi (równoległymi), jeśli linia reprezentująca dwa wektory jest równoległa.
Operacje wektorowe
Mnożenie przez skalar
Wektor można pomnożyć przez skalar, co daje również wektor, wynikowy wektor to:
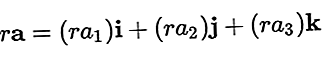
Dodawanie i odejmowanie wektorów
Jako przykład wektora za=za1ja + za2jot + za3k ib=b1ja + b2jot + b3k
Wynik a plus b to: 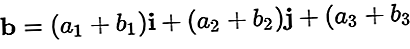
redukcja wektorów ma również zastosowanie poprzez zamianę znaku + na znak -